Číselné systémy a podmienky

Tri hlavné oblasti rozdielu od našich čísel

Predstavte si, aké jednoduchšie by bolo naučiť sa aritmetiku v prvých rokoch, ak by ste sa museli naučiť len písať riadky ako ja a trojuholník. To v podstate museli robiť starovekí mezopotámii, hoci ich občas menili, predlžovali, otáčali sa atď.

Na to nemali naše perá a ceruzky ani papier. Napísali s tým nástroj, ktorý by použili v sochárstve, pretože médium bolo hlina. Či je to ťažšie alebo ľahšie sa s ňou naučiť ako s ceruzkou, je to hodiť hore, ale zatiaľ sú v oddelení ľahkosti a majú sa naučiť iba dva základné symboly.

Ďalší krok hodí kľúč do oddelenia jednoduchosti. Používame a Základňa 10

V knihe „Pocta Babylonii“ [Matematický vestník, Zv. 76, č. 475, „Využitie dejín matematiky vo výučbe matematiky“ (marec, 1992), s. 158-178], spisovateľ-učiteľ Nick Mackinnon hovorí, že používa babylonskú matematiku na výučbu 13-ročných detí o základniach iných ako 10 rokov. Babylonský systém používa základňu 60, čo znamená, že namiesto desatinného čísla je to sexagesimálne.

Babylonský systém čísiel aj náš sa spoliehajú na to, že majú hodnotu. Dva systémy to robia inak, čiastočne preto, že v ich systéme chýbala nula. Učenie babylonského polohovacieho systému zľava doprava (od najvyššej po najnižšiu) pre prvý vkus základnej aritmetiky už pravdepodobne nie je ťažké než naučiť sa naše dvojsmerné, kde si musíme pamätať na poradie desatinných čísiel - zvyšujúce sa od desatinných miest, tie, desiatky, stovky a potom fúkajúce sa opačným smerom na druhej strane, nie je stĺp, iba desatiny, stotiny, tisíciny atď.

Na ďalších stránkach pôjdem do pozícií babylonského systému, ale najprv je potrebné sa naučiť niekoľko dôležitých čísel.

Hovoríme o obdobiach rokov pomocou desatinných množstiev. Máme desať rokov desať rokov, storočie 100 rokov (10 desaťročí) alebo 10X10 = 10 rokov na druhú a milénium 1000 rokov (10 storočí) alebo 10X100 = 10 rokov. Neviem o žiadnom vyššom termíne, ale nie sú to jednotky, ktoré používali Babylončania. Nick Mackinnon označuje tabletu od Senkareha (Larsa) od Sira Henryho Rawlinsona (1810 - 1895) * pre jednotky, ktoré používali Babylončania, nielen pre príslušné roky, ale aj z toho vyplývajúce množstvá:

1. FSS
2. ner
3. sar.

sossnersosssarsoss

Stále nie sú tie-breaker: To nemusí byť nevyhnutne ľahšie naučiť na druhú a krychlový rok odvodené termíny z latinčiny, ako sú jednoslabičné babylonské, ktoré nezahŕňajú kocky, ale množenie 10.

Co si myslis? Bolo by ťažšie naučiť sa základy čísiel ako babylonského školského dieťaťa alebo ako moderného študenta v anglicky hovoriacej škole?

* George Rawlinson (1812 - 1902), Henryho brat, ukazuje zjednodušenú prepisovanú tabuľku štvorcov v Sedem veľkých monarchií starovekého východného sveta. Tabuľka sa javí ako astronomická na základe kategórií babylonských rokov.

Všetky fotografie pochádzajú z tejto online naskenovanej verzie vydania Georga Rawlinsona z 19. storočia Sedem veľkých monarchií starovekého východného sveta.

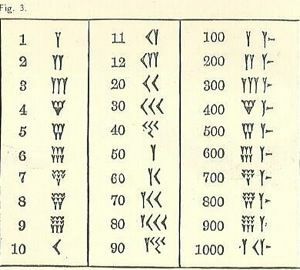
Keďže sme vyrastali s iným systémom, babylonské čísla sú mätúce.

Aspoň čísla bežia zhora zľava doprava, podobne ako náš arabský systém, ale ostatné sa pravdepodobne zdajú neznáme. Symbolom jedného je klinovitý tvar alebo tvar Y. Bohužiaľ, Y tiež predstavuje 50. Existuje niekoľko samostatných symbolov (všetky založené na kline a línii), ale všetky ostatné čísla sú z nich tvorené.

Pamätajte, že forma písania je klinový alebo klinovitého tvaru. Z dôvodu nástroja, ktorý sa používa na kreslenie čiar, existuje obmedzená rozmanitosť. Klin môže alebo nemusí mať chvost, natiahnutý ťahaním pera na písanie tvaru klinca pozdĺž hliny po vytlačení tvaru trojuholníka.

10, opísaná ako šípka, vyzerá trochu ako roztiahnutá.

Tri rady až 3 malých 1s (napísané ako Ys s niekoľkými skrátenými chvostami) alebo 10s (10 je napísané ako

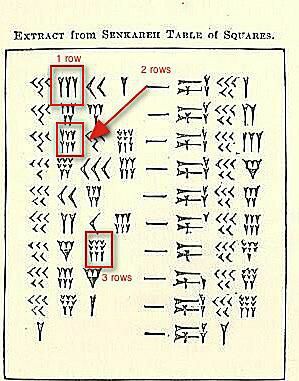
Existujú tri sady klínového čísla klastre zvýraznené na vyššie uvedenom obrázku.

Momentálne sa nezaujímame o ich hodnotu, ale o to, ako by ste videli (alebo písali) kdekoľvek od 4 do 9 toho istého čísla zoskupeného dohromady. Tri idú za sebou. Ak je štvrtá, piata alebo šiesta, ide nižšie. Ak existuje siedmy, ôsmy alebo deviaty, potrebujete tretí riadok.

Nasledujúce stránky pokračujú s pokynmi na vykonávanie výpočtov s Babylonskou klínovou pečaťou.

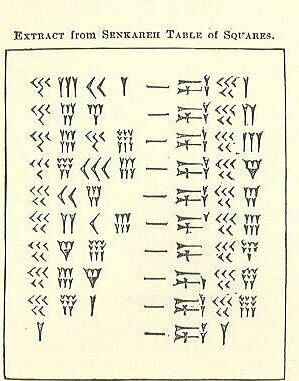
Z toho, čo ste čítali vyššie o FSS - na ktoré si budete pamätať, že Babylončan je už 60 rokov, klin a šípka - čo sú opisné názvy klínových značiek, aby ste zistili, ako tieto výpočty fungujú. Jedna strana čiarkovanej značky je číslo a druhá štvorec. Vyskúšajte to ako skupina. Ak to nedokážete zistiť, pozrite sa na ďalší krok.

Dokážete to zistiť hneď teraz? Dajte mu šancu.

...

Na ľavej strane sú 4 jasné stĺpce, za ktorými nasleduje znak podobný pomlčke a 3 stĺpce napravo. Pri pohľade na ľavú stranu je ekvivalentom stĺpca 1 s 2 stĺpce najbližšie k pomlčke (vnútorné stĺpce). Ostatné 2, vonkajšie stĺpce sa počítajú spolu ako stĺpec 60. rokov.

• 4-
• 3-Ys = 3.
• 40+3=43.
• Jediným problémom je, že za nimi je ďalšie číslo. To znamená, že to nie sú jednotky (miesto tých '). 43 nie je 43-tých, ale 43-60s, pretože je to sexagesimálny (základný-60) systém a je v FSS stĺpec podľa dolnej tabuľky.
• Násobením 43 x 60 získate 2580.
• Pridajte ďalšie číslo (2-
• Teraz máte 2601.
• To je štvorec 51.

Ďalší riadok má 45 v FSS stĺpec, takže vynásobte 45 x 60 (alebo 2700) a potom pridajte 4 zo stĺpca jednotiek, takže máte 2704. Druhá odmocnina 2704 je 52.

Dokážete zistiť, prečo posledné číslo = 3600 (60 štvorcov)? Tip: Prečo to nie je 3000?